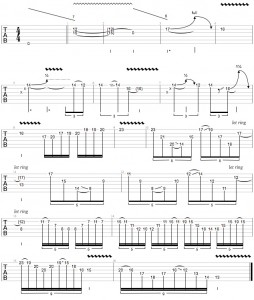
For this first column, I feel its best that we start off with something simple. The purpose of this column is to show which chords can be derived from the Major Scale, how one would come to these said chords and what possible tensions can be applied to each chord while remaining diatonic to the “mother” scale. A few things to note:
All examples can be transposed into any other key, though for the majority of this column I will be using C major as our primary scale, this will make the given information easier to digest.
The harmonization applied here will be tertian in nature, meaning we will be constructing chords with superimposed 3rds, as opposed to say, quartal or secundal harmonization, etc. (something we will touch upon in a later column.)
C Major Scale
Most readers will already be familiar with most major scales, and I am sure all will have heard/seen the C major scale before. For those who do not know, the Major scale is created by applying the following formula to a tonic (root): Whole step, Whole step, ½ step, Whole step, Whole step, Whole step, ½ step. Apply this to C and you get the following:

Triads
Now, how do we derive chords from this given scale? Further, how can we make sure these chords are diatonic to our mother scale? This is simple, lets start with the 7 triads found in C major:
triads

Here, we stack 3rds on each degree of the Major Scale until we have 7 triads:
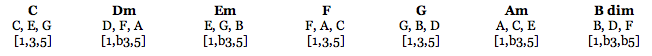
As you can see, we stacked these triads in 3rds as we discussed earlier, I feel it is important that the reader familiarize himself to tertian harmonization before he attempts to explore other possibilities. The reason for this is that most songs and pieces that musicians come across are constructed upon tertian harmonic structures, it is important to explore this type of harmonization in Tonal and Modal music before moving on to other types of harmonizations.
7 th Chords
Taking this idea 1 step further, let us harmonize to the next tertian scale degree so that we can get seven different diatonic 7th chords in our mother scale of C major.
7th chords

As you can see we now have seven different 7th chords diatonic to C major:

Tertian Clusters
Finally, lets take this principle all the way, and stack up the entire major scale onto itself, taking into consideration as always the tertian harmonization in question (again a limitation set for this column only). This is what you would get:
Diatonic Cluster


Now we have every possible diatonic tension stacked onto every scale degree. The applications of this idea are actually much more extensive than one would, at first, perceive. The main point to consider for its application to guitar is that obviously you will not be able to play any of these chords in their entirety, but that is not the point we are looking for per se.
With this outlook on diatonic harmony, one is free now to choose tensions that go with the basic triadic or 7th chord harmonizations. There are entire chapters of books written on the subject devoted to which tensions go best with which chords, but that is not what I would like to go into in this column.
Rather, I think its best that the reader attempt to play all voicings he can think of for each particular degree of the scale, listen to said voicings, and create a vocabulary of which chords he/she deems to be best or most suitable to his playing/composing style.
An example of possible chords on each scale degree, all diatonic to C major:
C: Cmaj7, Cmaj9, C (add9), C6/9…
D: Dm7, Dm9, Dm (add 9), Dm11, Dm6…
E: Em7, Em11, Em (add b13), Em11 (b13)…
F: Fmaj7, Fmaj9, Fmaj7 #11, Fmaj9 #11, Fmaj9 #11 13, Fmaj7 (13)…
G: G7, G9, G9 (13), G add9, G6/9…
A: Am7, Am9, Am11, Am (add 9)…
B: Bm7b5, Bm7b5 (add 11), Bm7b5 (add b13), B diminished [triad] (add b9)…
Again, some of these chords might sound terrible in one style and work perfectly well over another. Even more subjective: They may sound great to one reader and terrible to another, sound best in one register as opposed to another, once more the options become endless.
In the end, it is the composer/performer that needs to dive into the material and choose which voicings he/she will reject and which voicings he/she will apply to compositions and/or chordal vocabulary. The number of voicings open to the reader is staggering, but that is the beauty of it… one is not bound by anything but patience and imagination.
If there are any musical terms in this article that you are unfamiliar with, I recommend visiting Virginia Tech Multimedia Music Dictionary. Also, feel free to ask me any questions you might have regarding music theory in the Guitar Messenger Forum.
Roberto’s currently listening to: Stravinsky- Symphony of Psalms